
RUCH JEDNOSTAJNIE PRZYSPIESZONY Scenariusz lekcji fizyki z wykorzysteniem programu Microsoft Excel. Autor: mgr Jolanta Herzyk nauczyciel fizyki w Liceum i Gimnazjum Sióstr Urszulanek w Rybniku |
(Uwaga! -
niektóre symbole matematyczno - fizyczne
zostały zastąpione literami o zbliżonym wyglądzie: f
, [ , oraz A )
Temat: Ruch jednostajnie przyspieszony.
Cel lekcji: analiza
ruchu jednostajnie przyspieszonego na przykładzie wózka w dół
równi pochyłej i wykresów zależności
s = f (t), v =
f (t) oraz u
= f (t) sporządzonych
w programie Microsoft Excel.
Metoda prowadzenia lekcji: praktyczno - ćwiczeniowa
Wykorzystane materiały i środki dydaktyczne:
Plan lekcji:
| 1. (5 min) | Przypomnienie własności dotychczas poznanych ruchów. Zapisanie równań dotyczących ruchu ze stałym przyspieszeniem, które zostały wprowadzone na poprzedniej lekcji. |
| 2. (5 min) | Omówienie planu przebiegu lekcji, w tym doświadczenia, które zostanie przeprowadzone przez uczniów pod nadzorem nauczyciela. Uruchomienie komputerów i programu Microsoft Excel. |
| 3. (15 min) | Wykonanie doświadczenia z równoczesnym zapisywaniem wyników pomiarów w arkuszu kalkulacyjnym programu Microsoft Excel. |
| 4. (5 min) | Opracowanie za pomocą programu Microsoft Excel wykresów: s = f (t), v = f (t) oraz u = f (t). |
| 5. (10 min) | Sformułowanie wniosków wynikających z zaobserwowanych zależności. Wykonanie wydruku tabeli i wykresów. |
| 6. (5 min) | Zapisanie wniosków i podsumowanie lekcji. |
Wózek będzie startował z wierzchołka równi pochyłej:

Tabela pomiarów powinna zawierać:
| Lp. | t [ s ] | s [ m ] | a [ m/s ] | v [ m/s ] | As [ m ] |
| 1 | |||||
| 2 | |||||
| 3 | |||||
| ... |
Tabela pomiarów wykonanych przez uczniów:
| Lp. | t [ s ] | s [ m ] |
| 1 | 2 | 0,12 |
| 2 | 4 | 0,46 |
| 3 | 6 | 1,13 |
| 4 | 8 | 1,98 |
Wartości a, v obliczamy ze wzorów, poznanych na poprzedniej lekcji:
a = 2 . s / t2
v = a . t
gdzie:
a - przyspieszenie
s - droga przebyta przez wózek, w danym przedziale czasu t
t - dany przedział czasu
Tabela zawierająca wyniki pomiarów uzupełniona o obliczone wartości a, v oraz As
| Lp. | t [ s ] | s [ m ] | a [ m/s ] | v [ m/s ] | As [ m ] |
| 1 | 2 | 0,12 | 0,060 | 0,12 | 0,12 |
| 2 | 4 | 0,46 | 0,058 | 0,23 | 0,34 |
| 3 | 6 | 1,13 | 0,063 | 0,38 | 0,67 |
| 4 | 8 | 1,8 | 0,062 | 0,50 | 0,85 |
Pierwszym utworzonym wykresem jest wykres zależności s = f (t). Jak widać wyniki pomiarów wykonanych przez uczniów nie są dokładne, dlatego wykresy najlepiej sporządzić wybierając punktowy typ wykresów, a później samodzielnie nanieść odpowiednią krzywa lub prostą.
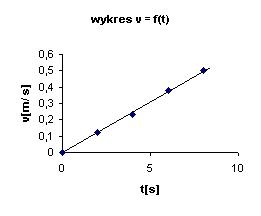
Z powyższego wykresu wynika, że prędkość wózka jest wprost proporcjonalna do czasu ruchu v ~ t (czyli prędkość wózka rośnie jednostajnie z czasem). Oznacza ta, że wózek porusza się ze stałym przyśpieseniem a = const, bo wartości przyrostów prędkości wstałych przedziałach czasu są stałe: A v / A t = const = a.
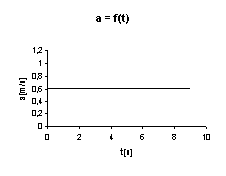
Powyższy wniosek potwierdza wykres zależności przyspieszenia do czasu a = f (t):
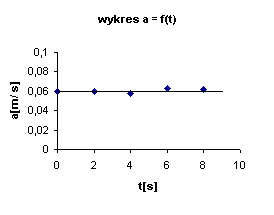
Skoro już wiadomo, że ruch wózka jest ruchem ze stałym przyspieszeniem i tym samym wiemy jak zmienia się jego prędkość z czasem, można zadać sobie pytanie jak zależy droga od czasu ruchu?
Dla uzyskania odpowiedzi sporządzamy wykres zalezności drogi od czasu s = f (t):
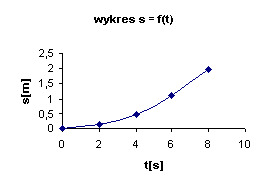
Wykres ten
pokazuje, że droga rośnie z kwadratem czasu ( s ~ t2
), ponieważ otrzymany wykres jest częścią paraboli,
co zgadza się z równaniem: s = a . t 2
/ 2.
Ponadto z analizy wartości przyrostów dróg As przebytych
przez wózek w kolejnych, jednakowych odstępach czasu ( tu 2s)
wynika, że drogi te mają się do siebie tak, jak kolejne liczby
nieparzyste 1 : 2 : 3 ...
Po sporządzeniu wykresów oraz przeprowadzeniu ich
analizy i sformułowaniu wniosków należy tabelę wraz z wynikami
wydrukować, a wnioski zapisać.
Wnioski:
Prędkość wózka rośnie jednostajnie z czasem czyli v~ t.
Wózek porusza się ruchem jednostajnie przyspieszonym ponieważ a = const.
Droga w ruchu jednostajnie przyspieszonym jest wprost proporcjonalna do kwadratu czasu s ~ t2 .
Drogi przebywane przez wózek w kolejnych, jednakowych odstępach czasu, mają się do siebie tak, jak kolejne liczby nieparzyste 1 : 2 : 3 ...
Poniżej przedstawię tabelę wyników idealnych dla przedstawionego doświadczenia oraz odpowiadające im wykresy.
| Lp. | t [ s ] | s [ m ] | a [ m/s ] | v [ m/s ] | As [ m ] |
| 1 | 2 | 0,12 | 0,06 | 0,12 | 0,12 |
| 2 | 4 | 0,48 | 0,06 | 0,24 | 0,36 |
| 3 | 6 | 1,08 | 0,06 | 0,36 | 0,69 |
| 4 | 8 | 1,2 | 0,06 | 0,48 | 0,84 |
Prędkość wózka rośnie jednostajnie z czasem czyli v ~ t
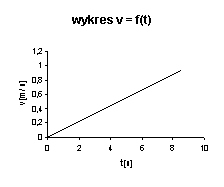
Wózek porusza się ruchem jednostajnie przyspieszonym ponieważ a = const
Droga w ruchu jednostajnie przyspieszonym jest proporcjonalna do kwadratu czasu s ~ t2 , co można wywnioskować z następującego wykresu s = f (t)
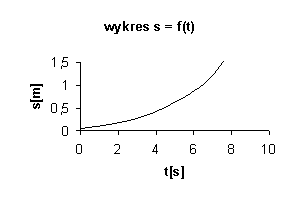
Jak widać otrzymane przez uczniów wykresy w oparciu o pomiary niewiele różnią się od powyżej przedstawionych wykresów teoretycznych zależności.
Gdy znane są wyniki, jakie powinno się otrzymać w sytuacji idealnej (zaniedbanie tarcia, niedokładności wyników pomiarów), można analizę otrzymanych przez uczniów wyników pomiarów poszerzyć o analizę błędów, wyznaczając w szczególności błędy bezwzględne, względne i procentowe.
Poniżej przedstawię krótką analizę błędów, którą uczniowie mogą także przeprowadzić w ramach zadania domowego. Nauczyciel podaje jedynie wzory umożliwiające obliczenie danego rodzaju błędów. Ponadto uczniowie powinni samodzielnie zastanowić się nad przyczynami otrzymanych błędów pomiarów.
Błąd bezwzględny - odchylenie wyniku pomiaru od wartości rzeczywistej, wyrażone w takich samych jednostkach, jak wielkość mierzona.
Wyznaczamy ten błąd dla wartości obliczonego przyspieszenia.
Aa1 = 0,00 m / s2
Aa2 = 0,002 m / s2
Aa3 = - 0,003 m / s2
Aa4 = - 0,002 m / s2
Błąd względny - jest to stosunek błedu bezwzględnego do wielkości mierzonej (jest wielkością niemianowaną).
[ Aa1/a1 ] = [ 0/0,6] = 0
[ Aa2/a2 ] = [ 0,002/0,058] = 0, 034
[ Aa3/a3 ] = [ - 0,003/0,063] = 0,048
[ Aa4/a4 ] = [ -0,002/0,062] = 0,032
Błąd procentowy - jest to błąd względny wyrażony w procentach.
Bpa1 = 0 %
Bpa2 = 3,4 %
Bpa3 = 4,8 %
Bpa4 = 3,2 %
Można również w ramach pracy dodatkowej zażądać od uczniów obliczenia wartości średnich danych wielkości oraz ich błędów.